GRAFICACION

martes, 17 de abril de 2012

3.3 REPRESENTACION TRIDIMENSIONAL DE OBJETOS

SUPERFICIES DE POLÍGONOS

Cualquier objeto tridimensional puede representarse como un conjunto de superficies poligonales planas. Para algunos objetos, como un polihedro, esto define precisamente las características de la superficie. En otros casos, una representación de un polígono ofrece una descripción aproximada del objeto. En la figura 1.1 se despliega un objeto solido modelado como una malla de superficies poligonales. Esta representación de la malla de polígonos puede desplegarse rápidamente para dar una indicación general de la estructura del objeto y la aproximación puede mejorarse dividiendo las superficies del objeto en caras poligonales menores.

Cada polígono de un objeto puede especificarse en un paquete de graficas mediante comando de líneas o de llenado de áreas para definir las coordenadas del vértice. Los paquetes CAD a menudo permiten a los usuarios introducir posiciones para el vértice junto con fronteras de polígonos con métodos interactivos. Estos vértices pueden representar el resultado de la digitalización de un trazo o bien pueden ser introducidos por un diseñador que este creando una nueva figura.

TABLAS DE POLÍGONOS

Una vez que el usuario haya definido cada superficie del polígono, el paquete de graficas organiza los datos de entrada en las tablas que utilizaran en el procesamiento y despliegue de las superficies. Las tablas de datos contienen las propiedades geométricas y de atributos del objeto, organizadas para facilitar el procesamiento. Las tablas de datos geométricos contienen coordenadas y parámetros de fronteras para identificar la orientación en el espacio de las superficies poligonales. La información de atributo del objeto incluye designaciones de cualquier modelo de color y sombreado que se aplicara a las superficies.

Los datos geométricos pueden organizarse de varias maneras. Un método adecuado para almacenar información de coordenadas consiste en crea tres listas: una tabla de vértices, una de aristas y una de polígonos. Los valores coordenados de cada vértice del objeto se almacenan en la tabla de vértices. La tabla de aristas enlistan los vértices extremos que definen a cada arista. Cada polígono se define en la tabla de polígonos como una lista de aristas componentes. Este esquema se ilustra la figura 1.2 para un objeto que consta de dos superficies poligonales. La tabla de polígonos contiene apuntadores que indican la tabla de aristas, la cual, a su vez, contiene apuntadores que señalan los valores coordenados en la tabla de vértices. Cuando en una escena se va a representar más de un objeto, cada uno puede identificarse en una tabla de objetos por medio del conjunto de superficies poligonales en la tabla de polígonos que definen a ese objeto.

El listado de los datos geométricos en tres tablas, como se muestra en la figura 1.2, ofrece una referencia adecuada de los componentes (vértices, aristas y polígonos) de un objeto. Así mismo, el objeto puede desplegarse eficazmente mediante el uso de datos de la tabla de aristas para trazar las líneas componentes. Sin la tabla de aristas, el objeto se desplegaría utilizando datos de la tabla de polígonos y esto quiere decir que algunas líneas se trazarían dos veces. Si tampoco se dispusiera de la tabla de vértices, la tabla de polígonos tendría que enlistar coordenadas explicitas de cada uno de los vértices de cada polígono. Toda la información referente a vértices y aristas tendría que reconstruirse a partir de la tabla de polígonos y las posiciones coordenadas se duplicarían para los vértices situados en la frontera de dos o más polígonos.

Podría incorporarse información adicional en las tablas de datos de la figura 1.2 para lograr una más rápida extracción de la información. Por ejemplo, podría extenderse la tabla de aristas para incluir apuntadores en la tabla de polígonos de modo que pudieran identificarse aristas comunes entre polígonos de mayor rapidez (fig. 1.3). Esto es particularmente útil cuando se aplican modelos de sombreado a las superficies, con los patrones de sombreado que varían ligeramente de un polígono al siguiente. Tambien podría ampliarse la tabla de vértices haciendo referencia cruzada de vértices para las aristas correspondientes.

Ya que las tablas de datos geométricos pueden contener listados extensos de vértices y de aristas de objetos complejos, es importante que los datos se verifiquen en consistencia y completitud. Cuando se especifican definiciones de vértices, líneas y polígonos, es posible que pudieran cometerse ciertos errores de entrada que distorsionarían el despliegue del objeto. Cuanta mas información se incluya en las tablas de datos, más fácil será verificarla. Algunas de las pruebas que podrían realizar un paquete de graficas son:

(1) Que todos y cada uno de los vértices se enliste como un extremo de cuando menos dos líneas.

(2) Que toda línea sea parte cuando menos de un polígono.

(3) Que todo polígono sea cerrado.

(4) Que cada polígono tenga al menos tenga un arista compartida.

(5) Si la tabla de aristas contiene apuntadores a polígonos, que toda arista referenciada por un apuntador de polígono tenga un apuntador reciproco hacia el polígono.

ECUACIONES DE PLANO

Los parámetros que especifican la orientación especial de cada polígono se obtienen de los valores coordenados de los vértices y las ecuaciones que definen los planos poligonales. Estos parámetros de planos se utilizan en transformaciones de visión, modelos de sombreado y algoritmos de superficies ocultas que determinan que líneas y planos se traslapan a lo largo de la línea de visión.

La ecuación de una superficie plana puede expresarse así: Ax + By + Cz + D = 0

Donde (x,y,z) es cualquier punto de plano. Los coeficientes A, B, C, D son constantes que pueden calcularse utilizando los valores coordenados de tres puntos no coloniales en el plano. Comúnmente, se usan las coordenadas de tres vértices sucesivos en una frontera de un polígono para hallar valores de estos coeficientes. Al denotar las coordenadas de tres vértices de un polígono como (x1, y1, z1), (x2, y2, z2) y (x3, y3, z3), se puede resolver el siguiente conjunto de ecuaciones planas simultáneas para las razones A/D, B/D y C/D:

(A / D)xi + (B / D)yi + (C / D)zi = -1 i = 1, 2, 3

Utilizando un método de solución como la regla de Cramer, se puede escribir la solución de los parámetros del plano en forma de determinantes:

Podemos ampliar los determinantes y escribir los cálculos de los coeficientes del plano en la forma explícita:

A = y1(z2 − z3 ) + y2 (z3 − z1) + y3(z1 − z2 )

B = z1(x2 − x3 ) + z2 (x3 − x1) + z3(x1 − x2 )

C = x1(y2 − y3 ) + x2 (y3 − y1) + x3(y1 − y2 )

D = −x1(y2z3 − y3z2 ) − x2 (y3z1 − y1z3 ) − x3(y1z2 − y2z1)

Los valores de A, B, C y D se almacenan en la estructura de datos que contiene la información de coordenadas y atributos referente al polígono definido en este plano.

La orientación de una superficie plana se especifica por medio del vector normal al plano, como se muestra en la figura 1.4.Este vector normal tridimensional tiene las coordenadas cartesianas (A, B, C).

Puesto que con frecuencia trabajamos con superficies poligonales que encierran un objeto interior, se necesita distinguir entre los lados de la superficie.

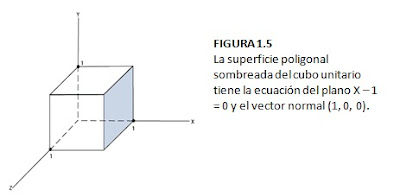
El lado del plano que da la cara al objeto interior se denomina “interior” y el lado visible o externo se llama “exterior”. Si se especifican vértices en un sentido igual al del reloj cuando se observa el lado externo del plano en su sistema coordenado por la derecha, la dirección del vector normal ira de adentro hacia afuera. Esto se demuestra para un plano de un cubo unitario de la figura 1.5.

Para determinar los componentes del vector normal de la superficie sombreada que se muestra en la figura 1.5, se seleccionan tres de los cuatros vértices situados a lo largo de la frontera del polígono.

Estos puntos se seleccionan en un sentido igual al del reloj cuando observamos el exterior del cubo hacia el origen.

Las coordenadas de estos vértices, en el orden seleccionado, se utilizan en la ecuacion de la figura 1.4 a fin de obtener los coeficientes del plano:

A = 1, B = 0, C = 0, D = -1. El vector normal de este plano esta en el sentido del eje x positivo.Las ecuaciones del plano se utiliza también para identificar puntos interiores y exteriores. Cualquier punto (x, y, z) exterior aun plano satisface la desigualdad.

Ax + By + Cz + D > 0

Análogamente, cualquier punto situado en el interior del plano produce un valor negativo de la expresión Ax + By + Cz + D. Para la superficie sombreada de la figura 1.5, cualquier punto exterior al plano cumple la desigualdad x - 1 < 0, mientras que cualquier punto interior al plano tiene un valor de coordenadas x menor que 1.

SUPERFICIES CURVAS

Los despliegues tridimensionales de las superficies curvas pueden generarse a partir de un conjunto de entrada de las funciones matemáticas que define las superficies o bien a partir de un conjunto de puntos de datos especificados por el usuario. Cuando se especifican funciones de curvas, un paquete puede emplear las ecuaciones definidoras para localizar y graficar posiciones de pixeles a lo largo de la trayectoria de la curva, casi igual como sucede con las curvas en dos dimensiones. Un ejemplo de la clase de superficies que pueden generarse a partir de una definición funcional se da en la figura 1.6. A partir de un conjunto de datos de entrada, un paquete determina las descripciones funcionales de la curva que mejor se ajusta a los puntos de datos según las restricciones de la aplicación. En la figura 1.7 se muestra un objeto cuyas superficies curvas pueden ser definidas por un conjunto de entrada de punto de datos.

Podemos representar una línea curva tridimensional en forma analítica con la pareja de funciones.

y=f(x), z=g(x)

Con la coordenada x seleccionada como variable independiente. Los valores de las variables dependientes y, z se determinan después a partir de las ecuaciones 1.6 a medida que se avanza a través de valores de x de un extremo de la línea al otro. Esta representación tiene algunas desventajas. Si se desea una grafica alisada, se debe cambiar la variable independiente siempre que la primera derivada (pendiente) de f(x) o bien g(x) se vuelve mayor que 1. Esto significa que se debe verificar continuamente los valores de las derivadas, que pueden volverse infinitas en algunos puntos. Asimismo, las ecuaciones anteriores ofrecen un formato desproporcionado para representar funciones con valores múltiples. Una representación más propicia de las curvas para aplicaciones de las graficas es en términos de ecuaciones paramétricas.

ECUACIONES PARAMÉTRICAS

Mediante la introducción de un cuarto parámetro, u, en la descripción coordenada de una curva, se puede expresar cada una de las tres coordenadas cartesianas en forma paramétrica. Cualquier punto de la curva puede representarse entonces por medio de la función vectorial.

P(u) = (x(u),y(u),z(u)

Por lo general, las ecuaciones paramétricas se constituyen de manera que el parámetro se defina en el intervalo de 0 a 1. Por ejemplo, una circunferencia en el plano xy con centro en el origen coordenado podría definirse en forma paramétrica como:

También son posibles otras formas paramétricas para describir circunferencias y arcos circulares.

En el caso de una curva arbitraria, puede ser difícil idear un conjunto de ecuaciones paramétricas que define completamente la forma de la curva. Pero cualquier curva puede aproximarse utilizando diferentes conjuntos de funciones paramétricas sobre partes diferentes de la curva. Por lo general estas aproximaciones se formar con funciones polinomiales. Dicha construcción por partes de una curva debe implantarse cuidadosamente para asegurar de que haya transición sencilla de una sección de la curva a la siguiente. La uniformidad de una curva puede describirse a partir de la continuidad de la curva entre las secciones. La continuidad de orden cero se refiere simplemente a que las curvas se interceptan. Continuidad de primer orden significa que las líneas tangentes (primeras derivadas) de dos secciones adyacentes de la curva son la misma en el punto de adyacencia. Continuidad de segundo orden quiere decir que las curvaturas (segundas derivadas) de las dos secciones de la curva son las mismas en la intersección. La figura 1.8 muestra ejemplos de los tres órdenes de continuidad.

Las ecuaciones paramétricas de las superficies se formulan con dos parámetros u y v. Una posición coordenada de una superficie se representa entonces por medio de la función vectorial paramétrica.

P(u,v) = (x(u,v), y(u,v), z(u,v))

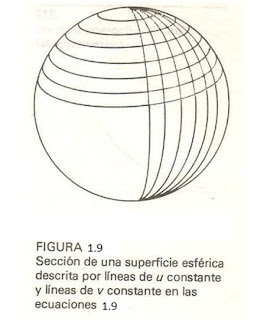
Las ecuaciones de las coordenadas x,y,z a menudo se acomodan de modo que los parámetros u y v están definidos dentro del intervalo de 0 a 1.Por ejemplo una superficie esférica puede describirse con las ecuaciones.

Donde r es el radio de la esfera. El parámetro u describe líneas de latitud constante sobre la superficie, mientras que el parámetro v describe líneas de longitud constante. Al mantener uno de estos parámetros fijo mientras se varía el otro sobre cualquier valor dentro del intervalo de 0 a 1, se podrían trazar líneas de latitud y longitud de cualquier sección esférica (fig. 1.9).

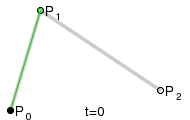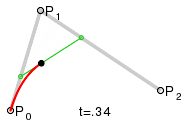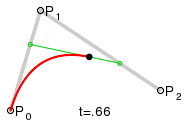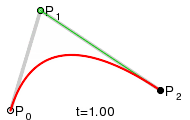
En aplicaciones de diseño, una curva o superficie a menudo se define especificando interactivamente un conjunto de puntos de control, los cuales indican la forma de la curva. Estos puntos de control son usados por el paquete para formar ecuaciones paramétricas polinomiales para desplegar la curva definida. Cuando la curva desplegada pasa a través de los puntos de control, como en la figura 1.10 se dice que interpola los puntos de control.

Por otro lado, se dice que los puntos de control se aproximan si la curva desplegada pasa cerca de ellos (fig.1.11). Existen muchas técnicas para constituir ecuaciones paramétricas polinomiales de curvas y superficies, dadas las coordenadas de los puntos de control. Entre los métodos básicos para desplegar curvas específicas con punto de control se incluyen las formulaciones de Bézier y “spline”.

INTEGRANTES:
SANTIGO CRUZ ROSA ELVIA
CARLOS DE LA CRUZ LORENA LIZETH
MENDOZA HERNANDEZ DAYSI YANET
OSORIO CRUZ ESMERALDA

BIBLIOGRAFIA:
GRAFICAS POR COMPUTADORA
DONAL HEARN/M.PAULINE BAKER
PAGINAS CONSUÑTADAS 204 - 211

jueves, 12 de abril de 2012

3.3.3 Superficies Cuadráticas

Una superficie cuadrática es la gráfica de una ecuación de segundo grado con tres variables x, y, z .

Elipsoide: Tiene ecuación

Es simétrico con respecto a cada uno de los tres planos coordenados y tiene intersección con los ejes coordenados en (a, 0, 0), (0, b, 0) y (0, 0, c). La traza del elipsoide sobre cada uno de los planos coordenados es un único punto o una elipse.

Paraboloide elíptico: Tiene ecuación

Sus trazas sobre planos horizontales z = k son elipses:

Sus trazas sobre planos verticales, ya sean x = k o y = k son parábolas.

Paraboloide hiperbólico: Tiene ecuación

Sus trazas sobre planos horizontales z = k son hipérbolas o dos rectas (z = 0). Sus trazas sobre planos verticales paralelos al plano x son parábolas que abren hacia abajo, mientras que las trazas sobre planos verticales paralelos al plano YZ son parábolas que abren hacia arriba. Su gráfica tiene la forma de una silla de montar.

Cono elíptico: Tiene ecuación

Sus trazas sobre planos horizontales z = k son elipses.

Sus trazas sobre planos verticales corresponden a hipérbolas o un par de rectas.

Hiperboloide de una hoja: Tiene ecuación

Sus trazas sobre planos horizontales z = k son elipses:

Sus trazas sobre planos verticales son hipérbolas o un par de rectas que se intersectan.

Hiperboloide de dos hojas: Tiene ecuación

Es una superficie con dos hojas (o mantos) separadas.

Sus trazas sobre planos horizontales z = k son elipses y sobre planos verticales son hipérbolas.

3.3.4 Representaciones de "Spline"

Un spline es una curva diferenciable definida en porciones mediante polinomios. Para el ajuste de curvas, los splines se utilizan para aproximar formas complicadas. La simplicidad de la representación y la facilidad de cómputo de los splines los hacen populares para la representación de curvas en informática, particularmente en el terreno de los gráficos por ordenador.

Curvas B-spline

Son los más utilizados en la práctica:

1. b-splines cuadráticos: fuentes True Type

2. b-splines cúbicos: los más comunes en programas de diseño gráfico.

En general, no pasan por ningún punto de control (ni siquiera los extremos), aunque se puede forzar que lo hagan.

principales ventajas sobre las curvas de Bezier:

1. Es de grado acotado ( aun definida por n puntos).

2. Sobre todo , mas apropiadas para el diseño interactivo: mas "suaves",control local.

Dado un conjunto de puntos P0,..., Pn, obtenemos una curva de aproximación compuesta por varios tramos, y las ecuaciones de cada tramo están influenciadas solamente por k vértices del polígono de control siendo k (orden de la B-Spline) un parámetro elegido a voluntad por el diseñador y, lógicamente, k ≤ n + 1:

Los parámetros que intervienen en una curva B-Spline se enumeran a continuación:

• P0,..., Pn, n+1 vértices o puntos de control.

• Ni,k: funciones B-Spline básica de orden k.

• d: grado de las B-Spline básicas (elección usual, d=3).

• k: orden de la B-Spline: k = d+1.

• Nº de tramos: n-d+1..

• Suavidad global de la curva: Ck-2 = Cd-1.

Propiedades

• No interpolan (salvo en P0, Pn, si así se especifica).

• Paramétricas P(t) = (x(t), y(t)).

• Suavidad Ck-2: k es el orden de la B-spline.

• No oscilan.

• Locales.

• Difíciles de calcular salvo casos especiales con fórmula matricial: B-Spline uniformes, Bézier.

• Mayor flexibilidad: elección de nodos permite más tipos de curvas.

3.3.5 Curvas y Superficies de Bézier

Pierre Bezier, ingeniero francés desarrollo este método de aproximación de spline para utilizarlo en el diseño de carrocerías de las automóviles Renault. Las spline de Bezier tienen varias propiedades que hacen que sean muy útiles y convenientes para el diseño de curvas y superficies.Asimismo, es fácil implementarla.Por estos motivos,las spline de Bezier están disponibles en forma común en varios sistemas de CAD, en paquetes generales de gráficas y en paquetes seleccionados de dibujo y pintura.

Curvas de Bezier

En general,es posible ajustar una curva de Bezier para cualquier numero de puntos de control.El numero de puntos de control que se debe aproximar y su posición relativa determinan el grado del polinomio de Bezier.

La idea de definir geométricamente las formas no es demasiado compleja: un punto del plano puede definirse por coordenadas. Por ejemplo, un punto A tiene unas coordenadas (x1, y1) y a un punto B le corresponde (x2,y2). Para trazar una recta entre ambos basta con conocer su posición.

Si en lugar de unir dos puntos con una recta se unen con una curva, surgen los elementos esenciales de una curva Bézier: los puntos se denominan puntos de anclaje o nodos. La forma de la curva se define por unos puntos invisibles en el dibujo, denominados puntos de control, manejadores o manecillas.

Curvas Lineales (Grado 1)

Sólo dos puntos de control ( P0 y P1).

Son líneas rectas.

Podemos recorrer la curva con un parámetro t є [0,1] que recorre la recta de P0 a P1.

La curva viene dada por la expresión:

B(t)= P0 + (P1 - P0)t = (1 - t)P0 + tP1 , t Є [0,1].

La t en la función para la curva lineal de Bézier se puede considerar como un descriptor de cuán lejos está B(t) de P0 a P1. Por ejemplo cuando T = 0.25, B(t) es un cuarto de la longitud entre el punto P0 y el punto P1. Como t varía entre 0 y 1, B(t) describe un línea recta de P0 a P1.

Curvas Cuadráticas (Grado 2)

Tres puntos de control (P0, P1 y P2).

Se construyen dos curvas lineales de Bezier entre P0-P1 y P1-P2.

Se construye una tercera curva lineal de Bezier entre las dos anteriores.

El t que recorre esta tercera recta, forma nuestra curva.

Una curva cuadrática de Bézier es el camino trazado por la función B(t), dados los puntos: P0, P1, y P2,

B(t) = (1 - t)^2 P0 + 2t (1 –t ) P1 + t^2 P2 , t Є [0,1].

Para curvas cuadráticas se pueden construir puntos intermedios desde Q0 a Q1 tales que t varía de 0 a 1:

* Punto Q0 varía de P0 a P1 y describe una curva lineal de Bézier.

* Punto Q1 varía de P1 a P2 y describe una curva lineal de Bézier.

* Punto B(t) varía de Q0 a Q1 y describe una curva cuadrática de Bézier.

Curvas Cubicas (Grado 3)

Cuatro puntos de control (P0, P1, P2 y P3).

Son las más utilizadas.

Se aplica el mismo principio de inducción, partiendo inicialmente de tres curvas de Bezier lineales.

Así se pueden generar curvas de cualquier grado.

La curva comienza en el punto P0 y se dirige hacia P1 y llega a P3 viniendo de la dirección del punto P2. Usualmente, no pasará ni por P1 ni por P2. Estos puntos sólo están ahí para proporcionar información direccional. La distancia entre P0 y P1 determina "qué longitud" tiene la curva cuando se mueve hacia la dirección de P2 antes de dirigirse hacia P3.

La forma paramétrica de la curva es:

B(t) = P0 (1 - t )^2 + 3P1*t (1 - t)^2 + 3P2*t^2 (1 - t) + P3*t^3 , t Є [0,1]

Propiedades de Bezier

1-El grado de la base de polinomios es uno menos que la cantidad de puntos de control.

2-El primer y último punto de la curva coincide con el primer y último punto del grafo de control.

3-El vector tangente en los extremos de la curva tiene la misma dirección que el primer y último segmento del grafo de control respectivamente.

4- Tienen control global.

Desventajas de las Curvas de Bezier

Para grafos de control complejos (formados por muchos puntos)

1- El grado de la base es elevado.

2- Tienden a suavizar demasiado la geometría del grafo de control.

3- Se tornan insensibles a pequeños cambios locales. El desplazamiento de un sólo punto de control casi no produce efecto en la curva.

4-El control global provoca que el desplazamiento de un sólo punto de control modifique a toda la curva.

Aplicaciones de las Curvas de Bezier

Las curvas de Bézier han sido ampliamente usadas en los gráficos generados por ordenador para modelado de curvas suaves. Como la curva está completamente contenida en la envolvente convexa de los puntos de control, dichos puntos pueden ser suavizados gráficamente sobre el área de trabajo y usados para manipular la curva de una forma muy intuitiva. Las transformaciones afines tales como traslaciones y rotaciones pueden ser aplicadas con gran facilidad a las curvas, aplicando las transformaciones respectivas sobre los puntos de control.

Superficies de Bézier

Se pueden utilizar dos conjuntos de curvas de Bézier para representar superficies de objetos especificados por punto de control de entrada. La función vectorial paramétrica de la superficie de Bézier se forma como el producto cartesiano de las funciones de combinación de Bézier:

Con Pj,k que especifica las localidades de los (m + 1) por (n + 1) puntos de control.

Ejemplo:

A continuación se ilustran dos trazos de superficies de Bézier. Los puntos de control están

conectados por líneas más delgadas y más gruesas muestran curvas con constantes u y v.

Cada curva de u constante se gráfica variando u con respecto al intervalo 0 a 1, con u fija en

uno de los valores en este intervalo unitario. Las curvas de u constante se trazan en forma

análoga.

Las superficies de Bezier tienen las mismas propiedades que las curvas de Bezier y ofrecen un método adecuado para aplicaciones de diseño interactivas.

Se ilustra una superficie formada con dos secciones de una superficie de Bézier.

Como sucede con las curvas, una transición sencilla de una sección a la otra se asegura

estableciendo continuidad de orden cero y de segundo orden en línea de frontera.

La continuidad de primer orden se obtiene eligiendo puntos de control a lo largo de una línea

recta que atraviesa la frontera y manteniendo una razón constante de segmentos de línea

colineales para cada una de estas líneas que cruzan la línea de frontera de la superficie.

En esta figura las superficies de Bézier son construidas con dos secciones de Bézier, unidas en la línea de frontera.

Las líneas punteadas conectan puntos de control especificados.

Se establece continuidad de primer orden haciendo la razón de la longitud “a” a la longitud “b” constante para cada línea colineal de puntos de control a través de la línea de frontera.

Propiedades de las superficies de Bézier

Las superficies de Bézier son una generalización natural de las curvas polinómicas, muchas de las propiedades de estas se mantienen.

La superficie sigue estando comprendida, si los pesos son todos positivos, en la envolvente convexa de la malla de control.

En el caso de superficies a trozos, cada tramo de superficie está además comprendida en la envolvente convexa de su malla de control.

Sin embargo, no hay una generalización sencilla de la propiedad de disminución de la variación. Es fácil, por ejemplo, comprobar que una recta puede cortar a la superficie en más puntos que los que corta al poliedro descrito por la malla de control.

Si queremos definir la parametrización en un recinto rectangular, [a,b]x[c,d] distinto del que sea empleado [0,1]x[0,1], no precisamos más que realizar una reparametrización afín de los parámetros u,v, que no afecta ni a la malla de control ni a la gráfica de la superficies

de modo que la nueva parametrización sea:

Del mismo modo que las curvas de Bézier sólo pasan por los vértices extremos, correspondientes a t = 0, t = 1, las superficies sólo pasan por cuatro vértices, las esquinas de la malla de control,

aunque la superficie pasa por las cuatro curvas de Bézier que describen los bordes de la malla de control.

Por ejemplo, para u = 0, la curva correspondiente, c(0,v), tiene por polígono de control {c_0,0,..., c_0,n}, la primera fila de la malla de control de la superficie. Del mismo modo, la última fila, {c_m,0,..., c_m,n}, es el polígono de control de la curva c(1,v). Y, para v = 0, el polígono de control de la curva c(u,0) es la primera columna de la malla de control, {c_0,0,..., c_m,0}.De manera análoga, el polígono de control de c(u,1) es la última columna, {c_0,n,..., c_m,n}.