GRAFICACION: 3.3.3 Superficies Cuadráticas

Una superficie cuadrática es la gráfica de una ecuación de segundo grado con tres variables x, y, z .

Elipsoide: Tiene ecuación

Es simétrico con respecto a cada uno de los tres planos coordenados y tiene intersección con los ejes coordenados en (a, 0, 0), (0, b, 0) y (0, 0, c). La traza del elipsoide sobre cada uno de los planos coordenados es un único punto o una elipse.

Paraboloide elíptico: Tiene ecuación

Sus trazas sobre planos horizontales z = k son elipses:

Sus trazas sobre planos verticales, ya sean x = k o y = k son parábolas.

Paraboloide hiperbólico: Tiene ecuación

Sus trazas sobre planos horizontales z = k son hipérbolas o dos rectas (z = 0). Sus trazas sobre planos verticales paralelos al plano x son parábolas que abren hacia abajo, mientras que las trazas sobre planos verticales paralelos al plano YZ son parábolas que abren hacia arriba. Su gráfica tiene la forma de una silla de montar.

Cono elíptico: Tiene ecuación

Sus trazas sobre planos horizontales z = k son elipses.

Sus trazas sobre planos verticales corresponden a hipérbolas o un par de rectas.

Hiperboloide de una hoja: Tiene ecuación

Sus trazas sobre planos horizontales z = k son elipses:

Sus trazas sobre planos verticales son hipérbolas o un par de rectas que se intersectan.

Hiperboloide de dos hojas: Tiene ecuación

Es una superficie con dos hojas (o mantos) separadas.

Sus trazas sobre planos horizontales z = k son elipses y sobre planos verticales son hipérbolas.

3.3.4 Representaciones de "Spline"

Un spline es una curva diferenciable definida en porciones mediante polinomios. Para el ajuste de curvas, los splines se utilizan para aproximar formas complicadas. La simplicidad de la representación y la facilidad de cómputo de los splines los hacen populares para la representación de curvas en informática, particularmente en el terreno de los gráficos por ordenador.

Curvas B-spline

Son los más utilizados en la práctica:

1. b-splines cuadráticos: fuentes True Type

2. b-splines cúbicos: los más comunes en programas de diseño gráfico.

En general, no pasan por ningún punto de control (ni siquiera los extremos), aunque se puede forzar que lo hagan.

principales ventajas sobre las curvas de Bezier:

1. Es de grado acotado ( aun definida por n puntos).

2. Sobre todo , mas apropiadas para el diseño interactivo: mas "suaves",control local.

Dado un conjunto de puntos P0,..., Pn, obtenemos una curva de aproximación compuesta por varios tramos, y las ecuaciones de cada tramo están influenciadas solamente por k vértices del polígono de control siendo k (orden de la B-Spline) un parámetro elegido a voluntad por el diseñador y, lógicamente, k ≤ n + 1:

Los parámetros que intervienen en una curva B-Spline se enumeran a continuación:

• P0,..., Pn, n+1 vértices o puntos de control.

• Ni,k: funciones B-Spline básica de orden k.

• d: grado de las B-Spline básicas (elección usual, d=3).

• k: orden de la B-Spline: k = d+1.

• Nº de tramos: n-d+1..

• Suavidad global de la curva: Ck-2 = Cd-1.

Propiedades

• No interpolan (salvo en P0, Pn, si así se especifica).

• Paramétricas P(t) = (x(t), y(t)).

• Suavidad Ck-2: k es el orden de la B-spline.

• No oscilan.

• Locales.

• Difíciles de calcular salvo casos especiales con fórmula matricial: B-Spline uniformes, Bézier.

• Mayor flexibilidad: elección de nodos permite más tipos de curvas.

3.3.5 Curvas y Superficies de Bézier

Pierre Bezier, ingeniero francés desarrollo este método de aproximación de spline para utilizarlo en el diseño de carrocerías de las automóviles Renault. Las spline de Bezier tienen varias propiedades que hacen que sean muy útiles y convenientes para el diseño de curvas y superficies.Asimismo, es fácil implementarla.Por estos motivos,las spline de Bezier están disponibles en forma común en varios sistemas de CAD, en paquetes generales de gráficas y en paquetes seleccionados de dibujo y pintura.

Curvas de Bezier

En general,es posible ajustar una curva de Bezier para cualquier numero de puntos de control.El numero de puntos de control que se debe aproximar y su posición relativa determinan el grado del polinomio de Bezier.

La idea de definir geométricamente las formas no es demasiado compleja: un punto del plano puede definirse por coordenadas. Por ejemplo, un punto A tiene unas coordenadas (x1, y1) y a un punto B le corresponde (x2,y2). Para trazar una recta entre ambos basta con conocer su posición.

Si en lugar de unir dos puntos con una recta se unen con una curva, surgen los elementos esenciales de una curva Bézier: los puntos se denominan puntos de anclaje o nodos. La forma de la curva se define por unos puntos invisibles en el dibujo, denominados puntos de control, manejadores o manecillas.

Curvas Lineales (Grado 1)

Sólo dos puntos de control ( P0 y P1).

Son líneas rectas.

Podemos recorrer la curva con un parámetro t є [0,1] que recorre la recta de P0 a P1.

La curva viene dada por la expresión:

B(t)= P0 + (P1 - P0)t = (1 - t)P0 + tP1 , t Є [0,1].

La t en la función para la curva lineal de Bézier se puede considerar como un descriptor de cuán lejos está B(t) de P0 a P1. Por ejemplo cuando T = 0.25, B(t) es un cuarto de la longitud entre el punto P0 y el punto P1. Como t varía entre 0 y 1, B(t) describe un línea recta de P0 a P1.

Curvas Cuadráticas (Grado 2)

Tres puntos de control (P0, P1 y P2).

Se construyen dos curvas lineales de Bezier entre P0-P1 y P1-P2.

Se construye una tercera curva lineal de Bezier entre las dos anteriores.

El t que recorre esta tercera recta, forma nuestra curva.

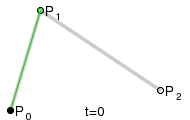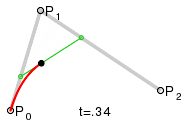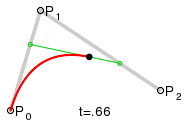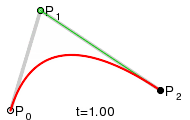
Una curva cuadrática de Bézier es el camino trazado por la función B(t), dados los puntos: P0, P1, y P2,

B(t) = (1 - t)^2 P0 + 2t (1 –t ) P1 + t^2 P2 , t Є [0,1].

Para curvas cuadráticas se pueden construir puntos intermedios desde Q0 a Q1 tales que t varía de 0 a 1:

* Punto Q0 varía de P0 a P1 y describe una curva lineal de Bézier.

* Punto Q1 varía de P1 a P2 y describe una curva lineal de Bézier.

* Punto B(t) varía de Q0 a Q1 y describe una curva cuadrática de Bézier.

Curvas Cubicas (Grado 3)

Cuatro puntos de control (P0, P1, P2 y P3).

Son las más utilizadas.

Se aplica el mismo principio de inducción, partiendo inicialmente de tres curvas de Bezier lineales.

Así se pueden generar curvas de cualquier grado.

La curva comienza en el punto P0 y se dirige hacia P1 y llega a P3 viniendo de la dirección del punto P2. Usualmente, no pasará ni por P1 ni por P2. Estos puntos sólo están ahí para proporcionar información direccional. La distancia entre P0 y P1 determina "qué longitud" tiene la curva cuando se mueve hacia la dirección de P2 antes de dirigirse hacia P3.

La forma paramétrica de la curva es:

B(t) = P0 (1 - t )^2 + 3P1*t (1 - t)^2 + 3P2*t^2 (1 - t) + P3*t^3 , t Є [0,1]

Propiedades de Bezier

1-El grado de la base de polinomios es uno menos que la cantidad de puntos de control.

2-El primer y último punto de la curva coincide con el primer y último punto del grafo de control.

3-El vector tangente en los extremos de la curva tiene la misma dirección que el primer y último segmento del grafo de control respectivamente.

4- Tienen control global.

Desventajas de las Curvas de Bezier

Para grafos de control complejos (formados por muchos puntos)

1- El grado de la base es elevado.

2- Tienden a suavizar demasiado la geometría del grafo de control.

3- Se tornan insensibles a pequeños cambios locales. El desplazamiento de un sólo punto de control casi no produce efecto en la curva.

4-El control global provoca que el desplazamiento de un sólo punto de control modifique a toda la curva.

Aplicaciones de las Curvas de Bezier

Las curvas de Bézier han sido ampliamente usadas en los gráficos generados por ordenador para modelado de curvas suaves. Como la curva está completamente contenida en la envolvente convexa de los puntos de control, dichos puntos pueden ser suavizados gráficamente sobre el área de trabajo y usados para manipular la curva de una forma muy intuitiva. Las transformaciones afines tales como traslaciones y rotaciones pueden ser aplicadas con gran facilidad a las curvas, aplicando las transformaciones respectivas sobre los puntos de control.

Superficies de Bézier

Se pueden utilizar dos conjuntos de curvas de Bézier para representar superficies de objetos especificados por punto de control de entrada. La función vectorial paramétrica de la superficie de Bézier se forma como el producto cartesiano de las funciones de combinación de Bézier:

Con Pj,k que especifica las localidades de los (m + 1) por (n + 1) puntos de control.

Ejemplo:

A continuación se ilustran dos trazos de superficies de Bézier. Los puntos de control están

conectados por líneas más delgadas y más gruesas muestran curvas con constantes u y v.

Cada curva de u constante se gráfica variando u con respecto al intervalo 0 a 1, con u fija en

uno de los valores en este intervalo unitario. Las curvas de u constante se trazan en forma

análoga.

Las superficies de Bezier tienen las mismas propiedades que las curvas de Bezier y ofrecen un método adecuado para aplicaciones de diseño interactivas.

Se ilustra una superficie formada con dos secciones de una superficie de Bézier.

Como sucede con las curvas, una transición sencilla de una sección a la otra se asegura

estableciendo continuidad de orden cero y de segundo orden en línea de frontera.

La continuidad de primer orden se obtiene eligiendo puntos de control a lo largo de una línea

recta que atraviesa la frontera y manteniendo una razón constante de segmentos de línea

colineales para cada una de estas líneas que cruzan la línea de frontera de la superficie.

En esta figura las superficies de Bézier son construidas con dos secciones de Bézier, unidas en la línea de frontera.

Las líneas punteadas conectan puntos de control especificados.

Se establece continuidad de primer orden haciendo la razón de la longitud “a” a la longitud “b” constante para cada línea colineal de puntos de control a través de la línea de frontera.

Propiedades de las superficies de Bézier

Las superficies de Bézier son una generalización natural de las curvas polinómicas, muchas de las propiedades de estas se mantienen.

La superficie sigue estando comprendida, si los pesos son todos positivos, en la envolvente convexa de la malla de control.

En el caso de superficies a trozos, cada tramo de superficie está además comprendida en la envolvente convexa de su malla de control.

Sin embargo, no hay una generalización sencilla de la propiedad de disminución de la variación. Es fácil, por ejemplo, comprobar que una recta puede cortar a la superficie en más puntos que los que corta al poliedro descrito por la malla de control.

Si queremos definir la parametrización en un recinto rectangular, [a,b]x[c,d] distinto del que sea empleado [0,1]x[0,1], no precisamos más que realizar una reparametrización afín de los parámetros u,v, que no afecta ni a la malla de control ni a la gráfica de la superficies

de modo que la nueva parametrización sea:

Del mismo modo que las curvas de Bézier sólo pasan por los vértices extremos, correspondientes a t = 0, t = 1, las superficies sólo pasan por cuatro vértices, las esquinas de la malla de control,

aunque la superficie pasa por las cuatro curvas de Bézier que describen los bordes de la malla de control.

Por ejemplo, para u = 0, la curva correspondiente, c(0,v), tiene por polígono de control {c_0,0,..., c_0,n}, la primera fila de la malla de control de la superficie. Del mismo modo, la última fila, {c_m,0,..., c_m,n}, es el polígono de control de la curva c(1,v). Y, para v = 0, el polígono de control de la curva c(u,0) es la primera columna de la malla de control, {c_0,0,..., c_m,0}.De manera análoga, el polígono de control de c(u,1) es la última columna, {c_0,n,..., c_m,n}.