Modelado: Se refiere al acto de dibujar la forma de un objeto en 3D. Está relacionado con la obtención de la forma y el volumen correctos. La información geométrica sobre un objeto es la parte más útil del total de la información sobre el objeto. En un modelo tiene sentido separar la información geométrica de los objetos, de la no geométrica. Bajo este planteamiento, al total de información del modelo informático se conoce como modelo del objeto, mientras que la informático exclusivamente geométrica constituye el modelo geométrico.
El concepto de modelado geométrico se refiere al conjunto de métodos utilizados para definir la forma y otras características de los objetos. La construcción de los objetos es normalmente, en si misma, una operación asistida por ordenador. Éstos juegan un papel primordial, ya que sin su potencia de cálculo los procedimientos del Modelado Geométrico solamente podrían aplicarse en modelos de escasa importancia práctica.
Evolución Histórica del Modelado Geométrico
Las raíces Modelo Geométrico se encuentran en los primeros sistemas gráficos, que fueron desarrollados al comienzo de la década de los 60 con la maquinaria numéricamente controlada (NC). El siguiente paso importante fue dado con el MIT, con el desarrollo de un compilador para un lenguaje de descripción gráfica (1967). Paralelamente, las principales multinacionales en los campos automovilísticos, aviación, etc. desarrollaron los primeros sistemas gráficos de diseño.
.
A mediados de los 70 se produjeron avances significativos, desarrollando nuevas técnicas, las cuales permitieron realizar lo que conocemos como superficies esculpidas, las superficies paramétricas, de Bezier, etc.
Mientras tanto, se desarrollaron los primeros modeladores alámbricos y los esquemas poligonales. Inicialmente estos sistemas fueron bidimensionales y trataban de implementar lo que se conoce como dibujo tecnico para ser realizado con un ordenador. Finalmente surgieron los esquemas de Modelo Sólido.
Modelado sólido
El modelado de sólidos es una rama del modelado geométrico que hace énfasis en la aplicabilidad general de los modelos, e insiste únicamente en la creación de representaciones "completas" de objetos físicos sólidos, esto es, representaciones que son adecuadas para la respuesta de preguntas geométricas arbitrarias de manera algorítmica.
Problemas a tratar en el modelado de sólidos
A continuación se presenta una breve descripción de los problemas a tratar dentro del modelado de sólidos.
1) Completitud
Los tipos mas simples de modelos de computadora de objetos fisicos, transfieren los metodos tradicionales utilizados en dibujo para crear modelos graficos bidimensionales a una computadora. Estos modelos consisten de objetos graficos bidimensionales tales como lineas, arcos, texto y otras primitivas de graficado requeridas por alguna figura.
Los modelos gráficos bidimensionales pueden ser actualizados o transformados a sus contrapartes tridimensionales, por medio de la adicción de información a través de la tercera coordenada, lo que resulta en una representación de sólidos conmúnmente denominada como modelo de alambres.
Desafortunadamente, aún una coleccion de líneas tridimensionales no es suficiente para representar una figura adecuadamente, porque algunas colecciones de líneas pueden tener muchas interpretaciones en términos de objetos sólidos.
2) Integridad
Para resolver los problemas de lineas y superficies ocultas, un paradigma en la metodologia de gráficas por computadora, es reemplazar los modelos gráficos por modelos de poliedros que proporcionen suficiente información para determinar las partes ocultas de los objetos. Estos modelos son constridos a partir de primitivas bidimensionales y caras poligonales en vez de sólo líneas.
El chequeo de la integridad (detección de intersecciones ilegales en la eliminacion de lineas ocultas, es solamente una solucion parcial al problema de integridad.
La integridad absoluta podría anular este problema haciendo la generacion de modelos incorrectos imposible, sin embargo, surge un nuevo problema: el proporcionar la integridad suficiente limita la facilidad de uso y la flexibilidad del sistema de modelado
3) Complejidad
El problema de los modelos gráficos es que no ofrecen información geométrica suficiente de la forma de un objeto, información que podría ser suficiente para calcular y dar respuestas a preguntas geometricas arbitrarias. Con todo, los modelos gráficos son perfectos y funcionan bien para la tarea para la que originalmente fueron desarrollados, a saber, la generación y representación de dibujos.
Aún un objeto relativamente simple como el dibujo de una casa de regular complejidad, puede requerir cientos de poligonos. Por otro lado, la cobertura geométrica de un modelo de poliedros no es suficiente para tareas que requieren de un modelado más exacto como superficies o formas curvas que requieren el diseño de la carroceria de un automovil por ejemplo.
4) Geometría computacional
Se espera que los modelos de sólidos sean capaces de proporcionar algorítmicamente respuestas a preguntas geométricas usuales que surgen en aplicaciones de la ingeniería. Ejemplos de tales preguntas se alistan a continuación:
- ¿ Como qué se ve el objeto?
- ¿ Cuál es el peso, superficie, área, etc. del objeto?
- ¿ Cuando este objeto lo suficientemente fuerte como para soportar esta carga?
El resultado de una pregunta geométrica puede ser una imagen, un número o una constante booleana (verdadero o falso).
Sistema de modelado de sólidos
El modelador de sólidos es un software que "negocia" con los modelos de sólidos y proporciona respuestas a preguntas geométricas.
Esquemas de representación de sólidos
La capacidad de una representación para codificar cosas que parecen sólidos no quiere decir que la representación sea adecuada para representar sólidos
El dominio de la representación debe tener el tamaño suficiente para permitir la representación de un conjunto útil de objetos físicos. La representación no debe ser ambigua, esto es, no deben existir dudas acerca de qué es lo que se está representando, y a su vez, una representación debe corresponder a un sólido y sólo uno. Cuando una representación es no ambigua, se dice que es una representación completa (completitud). Una representación es única, si se puede usar para codificar un sólido determinado en solamente una forma. Por otrol lado, una representacion precisa permite representar un objeto sim aproximaciones.
Un esquema de representación debe hacer imposible la creación de una representación invalida (que no corresponda a un solido).
Una representación debe ser compacta para ahorrar espacio y debe permitir la utilización de algoritmos eficientes para calcular las propiedades físicas de los objetos representados.
Dada la gran utilidad del modelado de sólidos en diversas áreas de la ciencia, han surgido diferentes esquemas de representación de sólidos.
Representación de fronteras (Boundary Representation - B-Rep)
Aquí el objeto es descrito en términos de los elementos de su superficie: vértices, aristas y caras, los cuales conforman su frontera.
El elemento que define a un sólido es la frontera, dado que separa el interior y el exterior del sólido. El interior y exterior significa dos conjuntos separados por un tercero: la frontera.
El esquema de representación de fronteras más ampliamente utilizado para los poliedros es el jerárquico, el cual contiene todas las coordenadas de los vértices junto con sus relaciones topológicas: las aristas que inciden en una cara y los vértices que conforman una arista.
El esquema de representación de fronteras es uno en el que la informacion geométrica viene dada de una manera explícita, por lo que la mayoría de los algoritmos de visualización basados en polígonos, trabajan sin problemas en él.
Geometría de construcción de sólidos ( Constructive Solid Geomtry- CSG)
Es un esquema en donde objetos sólidos simples (primitivas) son combinados por medio de operaciones booleanas regularizadas incluidas directamente en la representacion, para construir objetos más complejos a partir de objetos más simples.
Un objeto es almacenado como un árbol ordenado con operadores en los nodos internos y objetos simples en las hojas del árbol. Algunos nodos representan operadores booleanos, mientras que otros representan operaciones básicas, como las de traslación, rotacion y escalamiento. Las operaciones booleanas por lo general no son conmutativas, las aristas del árbol mantienen un cierto orden.
Para determinar las propiedades físicas o para crear imágenes, se deben combinar las propiedades de las hojas del árbol para obtener las propiedades de la raíz.
Las primitivas son solidos simples como cubos o esferas, para asegurar que todas las operaciones sobre dichos objetos, produzcan sólidos válidos.
Representaciones de partición espacial
En este tipo de representaciones, un sólido es descompuesto en una colección de sólidos adjuntos pero que no se intersecan, y que son más simples que el sólido original aunque no necesariamente del mismo tipo, ya que las primitivas de éstos pueden variar en tamaño, posición y orientación. Los esquemas más comunes de representación de partición espacial son:
Descomposición en celdas
Esta es una de las formas más generales de partición espacial. Cada sistema de descomposición de celdas define un conjunto de celdas primitivas que por lo general se parametrizan y con frecuencia son curvas. Esta representación proporciona una conveniente forma para compartir ciertas propiedades topológicas de los objetos.
La representación de descomposición en celdas no es ambigua, es posible que no sea única.
Enumeración de ocupación espacial
El sólido se descompone en celdas idénticas dispuestas sobre una malla regular fija. Estas celdas se denominan voxeles.
El tipo de celda más común es el cubo, y la representación del espacio como un arreglo regular de cubos se denomina cuberil. Cuando se representa un objeto con enumeración de ocupación espacial, sólo se controla la presencia o ausencia de una celda en cada posicion de la malla, de esta manera, un objeto se puede codificar como una lista única y no ambigua de celdas ocupadas.
La desventaja es que no existe el concepto de ocupación parcial, por lo que muchos sólidos, solo pueden aproximarse. Si las celdas son cubos, los unicos objetos que se pueden representar con exactitud son aquellos cuyas caras son paralelas a los lados del cubo y cuyos vértices pertenecen a la malla.
Árboles octales
Se derivan de los arboles de cuadrantes, que es un formato de representacion bidimensional utilizado para codificar imágenes.
Los arboles octales son un esquemas de representación de sólidos muy versátil y no ambiguo, además, con unos parámetros de resolución bien definidos, la representación que proporcionan es también única.
Modelado de superficie
Los modelos de superficie proporcionan información detallada de una superficie curva, pero no siempre dan superficie información para determinar todas las propiedades geométricas de un objeto limitado por la superficie.
Cuándo utilizamos los modelos de superficie:
- El objeto a representar es muy similar a una superficie: ejemplo una bandera, una lámina.
- Sólo nos interesa el aspecto externo del objeto.
Representación de Superficies
* Representación matemática de superficies:
- No paramétrica
P= [x,y,z]T= [ x,y,f(x,y) ]T
- Paramétrica
P(u,v)=[x,y,z]T=[ x(u,v), y(u,v), z(u,v) ]T
Ejemplo. Obtener la ecuación paramétrica y la información para almacenar en la base de datos de la superficie plana definida por los puntos P0(1,1,0), P1(5,1,0) y P2(1,9,0).
Solución:
P(u,v)= P0+ (P1 - P0)u + (P2- P0)v
P(u,v)= (1,1,0) + (4,0,0)u + (0,8,0)v
x=1 + 4u + 0v
y=1 + 0u + 8v
z=0 + 0u + 0v
0 ≤ u ≤ 1 , 0 ≤ v ≤ 1
Vectores tangentes unitarios
Pu / | Pu | = P1-P0 = (4,0,0) / 4= (1,0,0)
PV / | PV | = P2-P0 = (0,8,0) / 8= (0,1,0)
PROCESOS GENERATIVOS
MODELADO Y DE SOMBREADO Y COLOR
Un modelo de sombreado se utiliza para calcular la intensidad de la luz que debe observarse cuando se visualiza una superficie. Por último, se analizan la estructura y aplicaciones de los modelos de color que son de utilidad en los paquetes gráficas.
Modelado de intensidades de la luz
La intensidad de la luz se observa en cada superficie de un objeto depende del tipo de fuente de luz situadas en la vecindad y de las características de la superficie del objeto. Un modelo de sombreado para producir intensidades realistas sobre las superficies de un objeto debe tomar en consideración estas diversas propiedades.
Fuente de la luz
Las fuentes de luz que iluminan un objeto son de dos tipos básicos, las fuentes emisoras de luz y las fuentes reflectoras de luz. Entre las fuentes emisoras de luz se incluyen los focos y el sol. Las fuentes reflectoras de luz
son superficies iluminadas de otros objetos, como las paredes de un cuarto, que
están próximas al objeto que se está observando.
Las múltiples reflexiones de luz
que provienen de estos objetos cercanos se combinan para producir una
iluminación uniforme denominada luz
ambiente o bien luz de fondo.
Cuando las dimensiones de una
fuente de luz son pequeñas en comparación con el tamaño del objeto podemos
modelarlo como una fuente de punto. En
otros casos, se tiene una fuente de luz
distribuida. Esto ocurre cuando se tiene una fuente circunvecina grande, como
la lámpara de neón.
Las superficies de los objetos se iluminan con fuentes
emisoras de luz y fuentes reflectoras de luz.
Reflexión difusa
La luz disipada se denomina reflexión
difusa y se produce de la aspereza o
granulosidad de la superficie. Una superficie mate produce principalmente
reflexiones difusas, de manera que la superficie parezca igualmente brillante desde
todas las direcciones de observación.
Cada rayo de luz que cae en una partícula de la superficie
obedecerá la ley básica de la reflexión, pero como las partículas están
orientadas de manera aleatoria, las reflexiones se distribuirán de manera
aleatoria. Una superficie perfecta de reflexión difusa en la práctica
reflejaría la luz igualmente en todas direcciones, logrando una terminación
mate perfecta.
Reflexión difusa
Reflexión especular
La reflexión difusa y la fuente
de punto crean toques de luz o manchas brillantes, denominada reflexión especular. Este efecto de
toque de luz es más pronunciado en las superficies brillosas que en las
superficies opacas.
En ciertos ángulos de visión, una
superficie brillosa refleja toda la luz incidente, sin importar los valores de
la reflectividad. Este fenómeno, denominado reflexión especular, produce una
mancha de luz reflejada que es del mismo color que la luz incidente.
Normalmente, los objetos se iluminan con la luz blanca, de manera que la
reflexión especular es una mancha blanca brillante en relación con un reflector ideal (espejo
perfecto), el ángulo de incidencia y el ángulo de reflexión especular son iguales.
Reflexión especular
Luz reflectada
La luz que atraviesa una superficie se denomina luz transmitida o luz refractada. La refracción difusa y la refracción especular presentarse en las superficies de un objeto. Los objetos difusos son importantes cuando se va a modelar una superficie parcialmente transparente, como el vidrio empañado.
Los modelos realistas de materiales transparentes, como el vidrio lúcido, pueden crearse agregando contribuciones de refracción especular a los cálculos de la intensidad reflejada. Cuando la luz es incidente sobre una superficie transparente, parte de ella se refleja y otra parte se refracta. Ya que la velocidad de la luz es diferente en materiales distintos, la trayectoria de la luz refractada, especificada por el ángulo de refracción, es una función del índice de refracción de un material. Específicamente, el ángulo de refracción θ’ se calcula a partir del angulo de incidencia θ, el índice de refracción n del material del exterior de la superficie (por lo general aire) y el índice de refracción n’ del material de las superficies según la ley de la refracción:
n sen θ = n’ sen θ’
Patrones de textura y superficie
La textura de la superficie se necesita para modelar con exactitud objetos como paredes de ladrillo, caminos de grava y alfombras de pelo áspero. Además, algunas superficies contienen patrones que deben incluirse en el modelo de sombreado. La superficie de un florero podría contener un diseño pintado; un vaso para agua podría tener el escudo de la familia grabado en la superficie; una cancha de tenis contiene marcaciones de los pasillos, áreas de servicio y líneas de base; y una autopista de cuatro carriles tiene líneas divisorias y otras marcaciones, como derrames de aceite y rastras de ruedas.
Los valores de intensidad suministrados por un modelo de sombreado pueden ajustarse para acomodar la textura de la superficie alterando la normal a la superficie de manera que sea función de la posición sobre la superficie. Si permitimos que la normal a la superficie varié al azar, podemos obtener una superficie de textura irregular como la de una uva pasa. Puede utilizarse una función de repetición para modelar una superficie más regular, como una alfombra esculpida que contiene un modelo de textura repetido. Una superficie regular también puede modelarse dividendo la superficie en una colección de pequeñas superficies orientadas al azar.
También se utilizaran métodos de planimetría de texturas para modelar objetos. Los patrones pueden aplicarse a superficies de objetos tridimensionales con métodos análogos a aquellos que sirven para aplicar patrones a objetos bidimensionales. Un patrón de sombreado se define en un arreglo y el arreglo se mapea sobre un objeto en una posición designada. El patrón de arreglo puede considerarse como una superficie plana, y la posición y orientación del patrón puede especificarse en relación con el objeto para que contenga el patrón de textura. Esto se logra con comandos en una paquete de graficas para fijar el punto de referencia del patrón y dos vectores que definan la orientación del arreglo del plano, como las direcciones de los ejes x y y del arreglo.
La diferencia entre los objetos bidimensionales y tridimensionales es que ahora el patrón debe hacerse girar en torno al objeto tridimensional. Los planos del patrón pueden almacenarse y vinculase a las superficies indicadas del objeto de manera que puedan ser procesados por un método superficie oculta junto con las superficies del objeto. Los valores de intensidad almacenados en arreglos de patrones se utilizan para modificar o sustituir valores de intensidad calculados en el modelo de sombreado.
Sombras
Mediante la aplicación de un método de superficie oculta con una fuente de luz en la posición de visión, podemos determinar cuáles secciones de la superficie no deben “observase” desde la fuente de luz. Estos son las áreas de sombra. Una vez que se han determinado las áreas de sombra de todas las fuentes de luz, las sobras podrían considerarse como patrones de superficies y almacenarse en arreglos de patrones.
Objetos modelados con sombra
Despliegue de intensidades de luz
Los valores de la intensidad calculados por un modelo de sombreado para cada superficie de una escena deben convertirse en uno de los niveles de intensidad admisibles para el sistema de graficas particular en uso. Algunos sistemas pueden desplegar varios niveles de intensidad en forma directa, mientras que otros son capaces de desplegar solo dos niveles por cada pixel (encendido y apagado).
Asignación de niveles de intensidad
Los niveles de intensidades de pixeles admisibles de un sistema por lo general se distribuyen sobre el intervalo de 0 a 1. El valor 0 indica que una posición de pixel está apagada y el valor 1 significa la máxima intensidad. Todos los valores restantes se distribuyen en el intervalo de 0 a 1 de modo que la razón de intensidades sucesivas sea constante.
Medio tono
Cuando un dispositivo de salida de gráficas es capaz de desplegar solo dos niveles de intensidad por pixel (encendido y apagado), puede usarse un método de medio tono para suministrar las variaciones de intensidad de una escena. Cada posición de intensidad de la escena original se reemplaza por una retícula rectangular de pixeles. Este método se utiliza en la impresión para reproducir fotografías para publicarse en revistas, periódicos o libros.
Métodos de sombreado de superficies
Un modelo de intensidad puede aplicarse al sombreado de superficies en varias formas, según el tipo de superficie y los requisitos de una aplicación determinada.
Intensidad constante
En ciertas condiciones, un objeto con superficies planas puede sombrearse en forma realista utilizando intensidades de superficie constantes .En el caso donde una superficie se expone solamente a la luz ambiente y no se aplican diseños, texturas o sombras de superficie, el sombreado constante genera una representación exacta de la superficie.
Una superficie curva que se representa como un conjunto de superficies planas puede sombrearse con intensidades de superficie constante, si los planos que subdividen la superficie se hacen lo suficientemente pequeños.
La siguiente figura muestra un objeto modelado con sombreado constante.
Con este método, la intensidad se calcula en un punto interior de cada plano y toda la superficie se sombrea con la intensidad calculada. Cuando la orientación entre planos adyacentes cambia en forma abrupta, la diferencia en intensidades de superficie puede producir un efecto áspero e irreal. Podemos alisar las discontinuidades de intensidad en estos casos variando la intensidad sobre cada superficie de acuerdo con algún esquema de interpolación.
Sombreado de Gouraud
Este esquema de interpolación de intensidad, creado por Gouraud, elimina discontinuidades de intensidad entre planos adyacentes de la representación de una superficie variando en forma lineal la intensidad sobre cada plano de manera que los valores de la intensidad concuerden en las fronteras del plano. En este método, los valores de la intensidad a lo largo de cada línea de rastreo que atraviesan una superficie se interpolan a partir de las intensidades en los puntos de intersección con la superficie.
La siguiente figura demuestra este esquema de interpolación.
Este proceso se repite con cada línea que pasa por el polígono. En este método de interpolación, primero deben aproximarse las normales a la superficie en cada vértice de un polígono. Esto se logra promediando las normales a la superficie para cada polígono que contiene el punto de vértice, como se muestra en la siguiente figura. Estos vectores normales de los vértices se utilizan entonces en el modelo de sombreado para generar los valores de intensidad de los vertices.
Un ejemplo de un objeto de sombreado con el método de Gouraud.
Sombreado de Phong
Pueden hacerse mejoras a los modelos de sombreado de Gouraud determinando la normal aproximada a la superficie en cada punto a lo largo de una línea de rastreo y calculando después la intensidad mediante el uso del vector normal aproximado en ese punto. Este método, creado por Phong Bui Tuong, también se conoce como esquema de interpolación de vector normal. El automóvil es un ejemplo de la aplicación del sombreado de Phong.
Algoritmos de trazo de rayas
Puesto que podría generarse un número infinito de puntos de intensidad sobre las diversas superficies de una escena, un método para determinar las intensidades espectaculares en posiciones visibles de la superficie consiste en trazar rayas hacia atrás des la posición de visión hasta la fuente de luz. Esta técnica, conocida como trazo de rayas, se ilustra en la siguiente figura
Cuando se encuentran objetos transparentes en el proceso del trazo de rayas, las contribuciones de intensidad de la reflexión especular y la refracción especular se toman en cuenta. En una superficie transparente, la raya se divide en las dos componentes que se muestran en la siguiente figura. Cada raya se traza después en forma individual hacia su fuente.
Después que se ha procesado una raya para determinar todas las contribuciones de intensidad especular, se fija la intensidad del pixel correspondiente. La figura siguiente muestra dos vistas de una escena generada con técnicas de trazo de rayas.
Métodos del árbol octal
Los cálculos de la intensidad dependen de las normales a la superficie. Para incluir el sombreado de la superficie, necesitamos por tanto modificar los procedimientos que trasladan un árbol octal a un árbol cuádruple para su despliegue.
Asimismo, la normal a la superficie debe tener alguna componente en la dirección de la región vacía. Un algoritmo para verificar las regiones en torno a un voxel puede comenzar con el frente del árbol octal y examinar las cuatro zonas circunvecinas (izquierda, derecha, superior e inferior) que se muestra en la siguiente figura
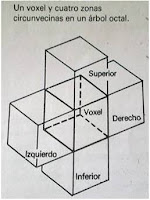
Suponiendo que todos los elementos de datos del árbol octal son homogéneos, la intensidad de un voxel visible no vacio se almacena en el árbol cuadruple para su despliegue. Este intensidad se calcula por medio de la funcion de iluminacion de intensidad utilizando informacion referente a las zonas situadas en torno al voxel. Los materiales transparentes se manejan superimponiendo intensidades de voxeles transparentes y de fondo en la misma posición del árbol cuádruple.
Modelo de color: es un método para explicar las propiedades o el comportamiento del dolor dentro de un contexto determinado.
Lo que se percibe como "luz", o diferentes colores, es una banda de frecuencia estrecha del espectro electromagnético.
Ondas de radio: son generadas por circuitos electromagnéticos u electrónicos como osciladores.
Microondas: abarcan la zona desde un mm hasta 30 cm. Son utilizados para los sistemas de radar y navegación.
Ondas infrarrojas: estas son producidas por cuerpos calientes y son absorbidas por la mayoría de los materiales.
Luz visible: es la parte del espectro que puede percibir el ojo humano.
Luz ultravioleta: es producida por el sol.
Rayos X y Rayos Gama: son ondas que dañan la estructura de los tejidos humanos.
PROPIEDADES DE LA LUZ
* Frecuencia dominante o matiz
* Luminancia o brillantez: cuanto mayor sea la intensidad (o energía), mas brillante se ve la fuente.
* Pureza o saturaciòn: la pureza describe la limpidez o cuàn "puro" se ve el color de la luz.
TRIANGULO DE CROMACIDAD
Es el diagrama cromático que muestra la composición del color.
Se considera como colores de la síntesis aditiva al rojo, verde y azul ya que con estos tres colores se obtienen los demás colores incluyendo al color blanco.
Modelo de color RGB
Nuestros ojos perciben el color a través de la simulación de tres pigmentos visuales. Estos pigmentos visuales tienen una sensibilidad pico en longitudes de onda cerca de 630 nm (rojo), 530nm (verde) y 450nm (azul). Esta teoría de la visión de tres estímulos es la base para desplegar salida de color en un monitor de vídeo mediante el uso de tres colores primarios rojo, verde y azul, conocido como modelo de color RGB.
Modelo de color CMY
Un modelo de color definido con los colores primarios azul.verde, magenta y amarillo (CMY) es útil para describir la salida de color de los dispositivos de copia dura.
Se incluye un punto negro ya que la combinación de azul-verde, magenta y amarillo comúnmente produce gris oscuro en vez de negro.
Modelo de color HSV
Este método emplea descripciones de color que tienen un aspecto mas intuitivamente para un usuario. En vez de escoger colores de acuerdo con sus componentes RGB. Los tres parámetros de color de este método que se presentan a un usuario se denominan hue, saturation y value (matiz, saturaciòn y valor), HSV.
INTEGRANTES
CODALLOS MOGOLLON MARTHA ANGELICA
MONTIEL SANTOS IMELDA
GARCIA DOMINGUEZ YULIANA ARELY
VALENTIN PAULA
BIBLIOGRAFIA
Donald Heam/ M.Pauline Baker. Gráficas por computadora 2a. Ed. Prentice Hall Hispanoamericana
John T. Demel/ Michael J. Miller. Gráficas por computadora. Mc Graw Hill
y que la imagen va
ser proyectada sobre el plano xy.
Si tenemos un punto
del objeto, queremos
determinar el punto proyectado 
.Empecemos por
definir las ecuaciones de la recta que pasa por un punto
y tiene la dirección
de las rectas de proyección. De forma paramétrica: 
y el punto del objeto
es
será el punto de
intersección de esta recta con el plano xy,
donde la coordenada z es nula.
,en coordenadas
homogéneas tendremos
que multiplicado por la
matriz anterior nos da 
